Doing the energy numbers for lifting way up
Probably not many people are much interested in how much energy it takes to lift something, starting, say a few planetary radii above the Earth. Still, if one needs to figure that out - as I once did over four decades ago - it might be nice to have some hints about how to do that. It is surprising to me that the calculation is still not readily available in the usual physics software nowadays.
I resist the urge to describe the long struggling search it took me to figure it out, back then. Nor tell you of the many uses I have had for the equation since then. My math skills are not easy for me, but sometimes one just has to do the numbers to show something very interesting can be done. (And unfortunately sometimes doing the numbers does not show that the something can be done; but, that is the way the cookie crumbles. There are lots of other things yet to explore; and one blocked path invites looking for another path toward the goal.)
Lifting something takes energy to do. And in lifting something a ways up, it gains energy thereby. The amount of effort exerted to get the mass lifted up there, however, can be considerably more than what is given to that which is raised up. For the following analysis, only the amount of energy that is received by the lifted mass, is what is of concern.
Lifting something up a short ways, we simplify the calculations. But if we are contemplating lifting something up a significant portion of a planetary radius or more, now we have to consider that the force of gravity varies with height above the planet. It is an inverse-square function kind of thing, meaning that if one squares - that is, multiply itself by its own self - the altitude in planetary radii, and take the inverse of that - meaning divide that quantity into 1, that gives one the gravitational force up at that number of planetary radii up there.
This means that figuring out how much energy it takes to lift something a specific distance, gets less the further one gets from the Earth - or other planetary body or moon. It takes doing the numbers to figure out exactly how much less, however. And that can be of interest if one is figuring out a rocket traveling up or figuring out an anchored tether space elevator. OK so not many people are interested in doing that, most likely. But to those who are, the following might save them lots of struggle in figuring out how do do that.
The task is to find out how much energy is given to a specific mass to lift it between two planetary radii altitudes. To lift it up from the ground, it is the difference between one planetary radius and the radius of its target altitude. Say, up to Geostationary Earth Orbit, from the ground.
Note that this is the energy to lift it straight up, not to put it in orbit up there.
The key to calculating the energy from one altitude to another, is to calculate the energy it takes to lift the mass to an infinite distance - an easy calculation - from one altitude, and then calculate the same thing only starting from the high endpoint altitude to an infinite distance, and subtract the two.
One can calculate the energy required to give the mass escape velocity starting from the upper altitude, from the escape velocity from the lower starting point, to get the result. But that is a way to check easier forms of calculation.
Remember, distances are considered straight up along a line to the center of the Earth or other planetary body, and expressed in terms of planetary radii. Thus, the ground level is a planetary radius of 1. Another example, for the Earth in 24 hour rotation, geostationary orbital altitude is about 6.6 radii.
So the asy equation is create a constant that is the product of the gravitational constant times the mass of teh earth (or other planet or moon) times the mass of the object being lifted. Then multiply that times the difference between the inverse ratios of the two altitudes expressed in planetary radii.
That is, Work (energy) = GMm((1/r0)- (1/r1))
I made a nice gif of the equation long ago, so here it is:
As an example taken from my web page http://www.kestsgeo.com/1techconcepts/energygroundtogeo/energygroundtogeo.html to use this to calculate the energy added to mass by lifting it from the ground straight up to geostationary earth orbit altitude:
W = GMm ((1 / R0) - (1 / RGEO))
W = (6.67E-11)(5.983E24)((1 / 6.378E6) - (1 / 4.23E7))
W = (4E14)(1.33E-7) = 5.31E7 Joules / Kg to GEO = 14.76 KwHr / Kg; @2.2 Kg / lbm = 6.71 KwHr per pound to GEO
That is the theoretical energy needed to lift one pound mass up to GEO; but to stay up there it also needs to be given orbital velocity, an additional 0.96 KwHr/ Kg to orbit at GEO (see the referenced web page to calculate that if need be.)
So, it is not that hard to calculate the energy given to the mass of an object lifted up to high altitudes.
Works on the lunar surface too, starting with the 1/6 earth gravity as the starting point. That is where I had to use this kind of calculation back circa 1970 as part of my hobby project to figure out if a tapered fiberglass anchored tether could be made of an existing material anchored on the moon and balanced weight across the Lagrange-1 point of the earth-moon system, between the Earth and the Moon. Months and months of tedious hand calculations back then, using a slide rule and doing the sums and difference by pen and paper, in my limited free time at home. Turned out, it could be done. But nobody cared back then but me; all the doers were too busy doing other things. As I said, that is the way the cookie crumbles; but in this case it is not the physics or the math that failed, it was the people stuff that failed to make the mark. Nowadays with a simple calculator one can do it easily, however. Works for Earth anchored tether space elevator calculations too.
I resist the urge to describe the long struggling search it took me to figure it out, back then. Nor tell you of the many uses I have had for the equation since then. My math skills are not easy for me, but sometimes one just has to do the numbers to show something very interesting can be done. (And unfortunately sometimes doing the numbers does not show that the something can be done; but, that is the way the cookie crumbles. There are lots of other things yet to explore; and one blocked path invites looking for another path toward the goal.)
Lifting something takes energy to do. And in lifting something a ways up, it gains energy thereby. The amount of effort exerted to get the mass lifted up there, however, can be considerably more than what is given to that which is raised up. For the following analysis, only the amount of energy that is received by the lifted mass, is what is of concern.
Lifting something up a short ways, we simplify the calculations. But if we are contemplating lifting something up a significant portion of a planetary radius or more, now we have to consider that the force of gravity varies with height above the planet. It is an inverse-square function kind of thing, meaning that if one squares - that is, multiply itself by its own self - the altitude in planetary radii, and take the inverse of that - meaning divide that quantity into 1, that gives one the gravitational force up at that number of planetary radii up there.
This means that figuring out how much energy it takes to lift something a specific distance, gets less the further one gets from the Earth - or other planetary body or moon. It takes doing the numbers to figure out exactly how much less, however. And that can be of interest if one is figuring out a rocket traveling up or figuring out an anchored tether space elevator. OK so not many people are interested in doing that, most likely. But to those who are, the following might save them lots of struggle in figuring out how do do that.
The task is to find out how much energy is given to a specific mass to lift it between two planetary radii altitudes. To lift it up from the ground, it is the difference between one planetary radius and the radius of its target altitude. Say, up to Geostationary Earth Orbit, from the ground.
Note that this is the energy to lift it straight up, not to put it in orbit up there.
The key to calculating the energy from one altitude to another, is to calculate the energy it takes to lift the mass to an infinite distance - an easy calculation - from one altitude, and then calculate the same thing only starting from the high endpoint altitude to an infinite distance, and subtract the two.
One can calculate the energy required to give the mass escape velocity starting from the upper altitude, from the escape velocity from the lower starting point, to get the result. But that is a way to check easier forms of calculation.
Remember, distances are considered straight up along a line to the center of the Earth or other planetary body, and expressed in terms of planetary radii. Thus, the ground level is a planetary radius of 1. Another example, for the Earth in 24 hour rotation, geostationary orbital altitude is about 6.6 radii.
So the asy equation is create a constant that is the product of the gravitational constant times the mass of teh earth (or other planet or moon) times the mass of the object being lifted. Then multiply that times the difference between the inverse ratios of the two altitudes expressed in planetary radii.
That is, Work (energy) = GMm((1/r0)- (1/r1))
I made a nice gif of the equation long ago, so here it is:
As an example taken from my web page http://www.kestsgeo.com/1techconcepts/energygroundtogeo/energygroundtogeo.html to use this to calculate the energy added to mass by lifting it from the ground straight up to geostationary earth orbit altitude:
W = GMm ((1 / R0) - (1 / RGEO))
W = (6.67E-11)(5.983E24)((1 / 6.378E6) - (1 / 4.23E7))
W = (4E14)(1.33E-7) = 5.31E7 Joules / Kg to GEO = 14.76 KwHr / Kg; @2.2 Kg / lbm = 6.71 KwHr per pound to GEO
That is the theoretical energy needed to lift one pound mass up to GEO; but to stay up there it also needs to be given orbital velocity, an additional 0.96 KwHr/ Kg to orbit at GEO (see the referenced web page to calculate that if need be.)
So, it is not that hard to calculate the energy given to the mass of an object lifted up to high altitudes.
Works on the lunar surface too, starting with the 1/6 earth gravity as the starting point. That is where I had to use this kind of calculation back circa 1970 as part of my hobby project to figure out if a tapered fiberglass anchored tether could be made of an existing material anchored on the moon and balanced weight across the Lagrange-1 point of the earth-moon system, between the Earth and the Moon. Months and months of tedious hand calculations back then, using a slide rule and doing the sums and difference by pen and paper, in my limited free time at home. Turned out, it could be done. But nobody cared back then but me; all the doers were too busy doing other things. As I said, that is the way the cookie crumbles; but in this case it is not the physics or the math that failed, it was the people stuff that failed to make the mark. Nowadays with a simple calculator one can do it easily, however. Works for Earth anchored tether space elevator calculations too.
Labels: Mooncable Project, space calculations, space elevators
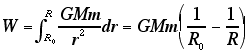

0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home